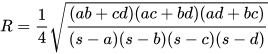أ. جمال البدراوي، وجمال الرياضيات

أ. جمال البدراوي، وجمال الرياضيات
في ربيع عام 1989م، كان لدينا، ضمن
مقرر مادة الرياضيات، درس بعنوان: "الشكل الرباعي الدائري"، الذين
هم من نفس جيلي يعرفون ذلك، (ربما خلت منه المقررات اليوم)، في تلك الفترة، أعتبر أنني
كنت محظوظًا أن التقيت أحد الأشخاص المؤثرين والمميزين للغاية، وهو الأستاذ (جمال عطية البدراوي)، والذي سرعان ما توطدت بيني وبينه علاقة أخوة، وصداقة حقيقية، كنت أمضي معه وقتًا في المذاكرة، والمطالعة، وحتى تناول الطعام، فضلًا بطبيعة الحال عن مناقشة كثير من الأمور.
كان (الأستاذ جمال) في الأصل يدرس مادتي الجولوجيا، والعلوم، وبشكل سهل، وممتع، وبطرائقه المميزة، وشغفه الواضح بتفاصيل الفن الذي كان يدرسه، وبقدرته (التخيلية)، على رسم الأشياء التي لم نكن نتصورها من قبل، (كالخلية الحية، وتركيب الذرة، والمجموعة الشمسية، وغيرها)، إذ استطاع أن يربط بين أشياء متباعدة، (من الذرة إلى المجرة)، وأن يقرب إلينا كثيرًا من المفاهيم، إلا أنه في الحقيقة بدا لنا "موسوعيًّا"، إذ كان يحب أن يجمع طلابه النابهين، ويشرح لهم، بالبراعة نفسها، مقررات مواد أخرى، كاللغة الإنجليزية، والرياضيات، وغيرها، بالإضافة بالطبع إلى مادته الأساسية، (مادة العلوم).
التقط الأستاذ جمال يومًا (من صفحة التدريبات غير المحلولة)، في كتاب الرياضيات مسألة، كان المطلوب فيها، هو أن تنظر إلى الرسم الموضح بالرسم، وتفهم المعطيات، ثم تثبت بالبرهان ما إذا كان "الشكل" الذي أمامك هو "شكل رباعي دائري"!
ولأنه كان يعتبرني أحد طلابه المميزين في مادة الرياضيات؛ فقد جاءني في الفصل، واستأذن من معلمي بالخروج معه، وتحدث معي في "الساحة" للحظات، ثم أعطاني "المسألة"، وطلب مني أن أحاول حلها، كما أعطاني معها شيئًا آخر، لم يبخل على أحدٍ من زملائي مرة به، وهو الإحساس بالتحدي اللازم، والاهتمام المطلوب، ولعل هذا هو الشيء الذي ربما أكون قد حاولت أنا أن أصنعه قارئي، في هذا الكتاب، وأنا أناقشه في بعض الأفكار، وأطرح عليه بعض "الأسئلة"، وأجعل المساحة أمامي وأمامه كافية؛ لطرح الإجابات المدهشة، والاحتمالات غير المتوقعة، وإيجاد الحلول!
كان الأستاذ جمال إنسانًا محبوبًا، وواثقًا بنفسه، ويمتلك حس الدعابة الذي ينبغي أن يمتلكه كل محب للرياضيات والعلوم، مجرد وجوده كان يبعث على اليقظة والبهجة، وربما كان هذا سببًا لشعور الكثيرين تجاهه بشيء ما من الغيرة. كنت أرى بعضهم أحيانًا ينالون منه بتلميحاتهم، ومع ذلك فهم لا ينكرون ما يشعرون به من إعجاب بشخصه.
في خلفية الأحداث لم أكن أعلم أن ثمة نقاشًا محتدمًا، كان يدور بينه، وبين معلمي الرياضيات الثلاثة بالمدرسة، حول نفس المسألة، وكان غريبًا حين عرفت بعد ذلك أنهم ثلاثتهم لم يصل أحد منهم إلى حلها، حين انتهى اليوم الدراسي؛ رجعت إلى البيت، ودخلت غرفتي، وأخرجت قلمي، وكمية مناسبة من الأوراق، وبدأت أرسم الشكل الرباعي بنفسي من جديد، وكان لديَّ حدس قوي، بأنني لن أستغرق في حل هذه المسألة سوى دقائق معدودة، بناء على ما مر بي من مسائل مشابهة، ومن ثم بدأت أركز، في المعطيات، وأحدد الشرط، وأضع فرضية، أو أقسم زاوية، أو أمد خطًّا، يصل ما بين أحد رؤوس الشكل، والنقطة (م)، في مركز الدائرة.
لم أكن يومها بحاجة إلى أن أعرف بعض المسميات التي عرفناها لاحقًا، مثل "مبرهنة براهما جوبتا، Brahmagupta's theorem والتي تنص على أنه إذا كان لرباعي دائري أقطار متعامدة؛ فإن العمود المنشأ من نقطة تقاطع أقطار المضلع على أحد أضلاعه سوف ينصف الضلع لمقابل بالتأكيد، (والعكس صحيح)، ولم أكن بحاجة أيضًا إلى نحفظ اسم العالم الهندي فتاسِّيري پاراميشڤارا، ومعادلته في إيجاد نِصفِ قطر الدائرة المحيطة بدلالةِ أطوالِ الأضلاعِ ونصف المحيط، ولا ما هو "القطع البديل" بل كنا نتدرب على ما يوصل إلى ما توصلا إليه من خلال الحلول، المهم هو أنني عملت كل ما يلزم مستفيدًا، من معارف متاحة أو سابقة، لكنني، وبعدما تكدست العديد من الأوراق أمامي بالكتابة، لم أصل إلى النتيجة، ولم أستطع إثبات المطلوب، وأدركت أن حدسي كان خاطئًا، وأن محاولتي الأولى كانت فاشلة تمامًا!
وبدأت من جديد في محاولة ثانية، بأن أرسم الشكل، وأمضي في الخطوات، بطريقة الاستلزام المنطقي: (بما أنَّ - إذًا)، إلا أن المحاولة الثانية هي الأخرى باءت بالفشل، ثم تكررت بعدها محاولات عديدة، لا أستطيع حصرها، كنت في كل مرة أكرر خطواتي، كما هي، ثم أغير منها خطوة واحدة على الأقل، ومع ذلك كنت لا أصل إلى المطلوب.
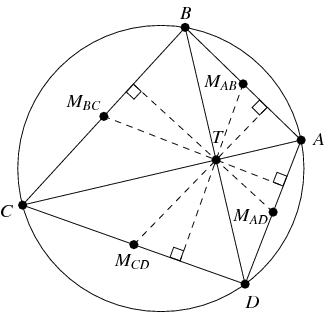
(مبرهنة براهما جوبتا Brahmagupta's Theorem)
(معادلة بارا ميشيفارا)
ومرت فترة من الوقت، وأنا على تلك الحال؛ حتى شعرت بأنني "عالق"؛ إلى أن ومضت في رأسي فكرة معينة، كانت عبارة عن عمل بسيط، أقوم به؛ فيؤدي بدوره إلى نتيجة، يسهل فهمها، (من زاوية حادة للغاية، أسقطت عمودًا، على أحد الأضلاع)، وفجأة استطعت أن أربط بين المعطيات، والحقائق الرياضية التي سبق لي فهمها، لكن بطريقة مختلفة، ومن ثم أعطيت للمجهول قيمته؛ حتى استطعت أن أثبت أن الشكل الذي أمامي في الرسم، هو "شكل رباعي دائري" في النهاية، وكان ذلك حدثًا مهمًا بحد ذاته.
ما أدهشني، في الأمر، هو أن الحل كان أمامي طيلة الوقت، وكان واضحًا، ولكني لم أكن أراه، معظم الحقائق العلمية المكتشفة كذلك، «دائمًا ما تكون واضحة جدًّا، وبسيطة؛ لدرجة أننا نتساءل: لماذا تأخر الاكتشاف كل هذا الوقت»[1].
كانت سعادتي حينئذ، بالحل غامرة، وإن كانت الخطوات المكتوبة طويلة بالنسبة إلىَّ، وإلى أي مسألة أخرى، قمت في السابق بحلها، وهو ما استدعى مني أن أعود إلى الخلف، وأنظر مرة أخرى في الحل المكتمل، وأتحقق من خطواتي جيدًا، لمعرفة ما إذا كان ثمة أمر ما، ما زال مخبّأ، أو أن أمرًا ما قد فاتني، في هذه اللحظة، وكأي إنسان طبيعي، لم أكن أفكر في تحسين الحل، وإنما كنت أحاول فقط ألا أنسى؛ لأن أي خطوة، من بين الخطوات، قد تهرب مني؛ فسوف تؤدي حتمًا، إلى فقدان الحل كله، أو نسيان باقي التفاصيل!
[1]
Vash Young, A fortune to share (Lulu. com, 2009), p. 30.
في اليوم التالي، كان أول شيء صنعته هو أن التقيت بالأستاذ جمال، وعرضت عليه حل المسألة، كنت معه شديد التركيز، وحرصت على أن أبقى واثقًا، ومتناغمًا، وأن يتدفق شرحي بسلاسة، وكأني أسرد له قصة ذات حبكة متماسكة؛ لأنك، وفق مقولة منسوبة إلى أينشتاين: «إذا لم تستطع شرحها، ببساطة؛ فأنت لا تفهمها جيدًا بما يكفي»[2]، وكانت سعادته بي، كبيرة للغاية، فما كان منه إلا أن التزمني، وقبَّل رأسي، (كما كان يفعل عادة، حين ألقاه، أو حين أقدم عملًا، يسره)، ثم إنه فاجأني بوجود حل آخر لديه، هو أبسط من حلي بخطوة واحدة، لهذا بدا أكثر تركيزًا، واهتمامًا أثناء عرضي الحل الذي توصلت إليه بنفسي؛ كونه يختلف في بعض الخطوات عن حله، ثم قال لي باسمًا: لا تخبر أحدًا بحلك؛ حتى أسمح لك بذلك.
[2]
Sidney I. Dobrin, and Kyle Jensen, eds. Abducting Writing Studies (SIU Press, 2016), p. 114; David Lindsay, Scientific writing: thinking in words (Csiro Publishing, 2020), p. 146.
ويبدو أنه كان قد عزم النية، على استكمال خطته، فقد ذهب، إلى زملائه الثلاثة، وكانوا قريبين مني، بما يكفي؛ لأعرف، في وجوههم، الحرج الذي تسبب فيه هذا التحدي لهم، كان هؤلاء الأربعة، بمن فيهم أستاذ جمال، أشخاصًا رائعين وودودين للغاية، وتقبلوا منه الأمر بدهشة، وقد لمحت، أثناء استعراضه الحل، فيما بينهم، أنه كان يمازحهم، بين لحظة، وأخرى، بطريقته، كما كان يضغط، إلى حد ما، على أعصابهم!
في "الشكل الرباعي الدائري" أنت تستطيع ببساطة إعطاء رمز لكل رأس، من رؤوسه الأربعة، ابدأ الحل بأي منها من دون مفاضلة، ليست هناك زاوية للنظر هي أفضل من غيرها؛ كي تبدأ بها أولًا، قد يكون أحد رؤوس الشكل هو أبعد في الرسم عن الرؤوس الثلاثة الأخرى، فيبدو غريبًا، ومنفردًا، وربما يبدو حاد الزاوية أكثر، لكنه يظل مثل باقيها، لا بد له من أن يقع في النهاية على محيط الدائرة، كما أنه ليس في الآية قراءة هي أفضل من الأخرى، المهم أنه في حال الجمع بينها في عملية التأويل، ينبغي أن يجري ذلك، في سياق النص، لا خارجًا عن محيطه؛ ستقول لي: "واو! هذا ما كنت تقصده إذًا، بتلك القصة المشوقة"!
حقيقة الأمر ليست كذلك، لقد أردت من القصة أشياء أخرى، لكني خمنت أنك قد تلمح التشابه الظاهر، ولم أشأ أن أتكتم على الأمر، القصة قد تجعل جميع حواسك حاضرة، تجعل ذهنك مهيّأ لتقبل كثير من المعلومات، والربط بينها، وفهمها بطريقة ممتعة، (قصة موسى، في حد ذاتها مثال بديع، على ذلك)؛ ولكي تعرف أنني لم أكن أنوي استغلال التشابه الحاصل بين الشكل الرباعي الدائري الذي دارت حوله القصة، والقراءات الأربع الواردة، وأنني قد أردت من القصة أشياء أخرى، يفترض بها أن تكون ذات صلة؛ سأطرح عليك هذا السؤال: "ماذا لو كانت الآية التي نتأملها، قد ورد فيها ثلاث قراءات، بدلًا من أربعة؟"
في هذه الحالة، كنت سأضطر إلى تعديل "غير مؤثر"، في الأحداث، يتمثل في عنوان الدرس الذي بنيت عليه حكايتي، (مساحة المثلث كمثال)؛ وذلك؛ حتى يحدث الربط بين عدد الرؤوس في الرسم، وعدد القراءات في الآية، (كل مثلث بالمناسبة له دائرة محيطة)؛ بما يعني أن الطريقة تعمل، ومع ذلك، فالتشابه الأول ربما يروق لك أكثر، وقد كان بإمكاني أن أستغله، في إقناعك، لكن مرادي من القصة هو أن أساعدك، لا أن أخدعك. ويبقى الأصل، حينما أسرد لك قصة، هو أن تعرف المراد منها بسهولة، ولو بجهد مقبول تبذله، وأن يكون المغزى هو أشبه شيء بتلك "الرسوم التوضيحية" التي أضعها لك في هذا الكتاب! فما الذي أردته من سرد تلك القصة إذًا؟!
إنني على مدار الكتاب، لا أفتأ أكرر عليك أسئلة ما بعينها، وأطرحها بطريقة تبدو في بعض الأحيان كما لو كانت "تحريضية"، كتلك الأسئلة التي تدور تحديدًا حول السبب في نزول قوله تبارك وتعالى: (إن هذان لساحران)، على أربع قراءات، وليس على قراءة واحدة، وسر هذا ببساطة يكمن في أنني أريد أن أثير فضولك، وأن أخلق لديك التحدي اللازم، والاهتمام المطلوب، وأن أريك "الطريقة"، ولعل هذا، من أوضح ما يمكن للقصة، أن تخبرنا به!
ثمة أمر جوهري أشد خطرًا، أريد أن أنبه إليه، ولكن بشكل "عكسي"، وهو ألا تنظر في القراءات الأربع الواردة في الآية، كما لو كان وجودها لغزًا رياضيًّا، يصعب حله، (هذا الشيء قد يبدو على العكس تمامًا مما تريد القصة قوله)، يمكن أن ترى ذلك في مرحلة، لكن ليس معنى هذا أن تتعامل، مع الأسئلة التي أطرحها عليك، كما تتعامل مع لغز مبهم، وليس معنى أنني سوف أتوصل إلى حلٍ أنه لم يعد بإمكانك أن تحصل على حل أفضل، أو مثله، وليس معنى أنني قد وصلت إلى حلٍ «أنني أذكى من غيري، هذا غير صحيح، كل ما هنالك، هو أنني أقضي مع الأسئلة وقتًا أطول»[3] أما بالنسبة إلى القرآن، فهو كتاب ميسر للذكر، و"الذكر" نشاط لغوي، وعقلي، إنه في الأساس أعمق من كونه تحريك لسانك بالكلمات، إنه عملية مرتبطة بالقراءة، والوعي، وجلاء المعنى، والحكمة من قوله تعالى: (طه ما أنزلنا عليك القرآن لتشقى) ينبغي أن تظل دومًا، في رحلة التأويل ماثلة!
القصة تعطينا إذًا فكرة سهلة عن "متعة الفهم"، والكتاب كله يحاول أن يفعل ذلك، أن تفكر في كل شيء بطريقة مختلفة، ومنطقية في الوقت نفسه، وأن تبذل الجهد المقبول، لا القليل الذي يعني كسل العقل، وخموله، ولا الزائد عن الحد لدرجة التكلف، والشطح بعقلك خارج دائرة النص، ثمة أشخاص رائعون، لكنهم حين يتعلق الأمر بالتراث، ينقصهم الشغف؛ لأن الحصول على الدهشة في كل ما هو "قديم"، بذات "الطرق القديمة" لا يأتي عادة، من دون تكلفة.
[3]
المقولة، بتصرف، لأينشتاين، انظر:
Carlo Cellucci, The making of mathematics: Heuristic philosophy of mathematics, Vol. 448. (Springer Nature, 2022), p. 52.
اعرف الفائدة المرجوة، من كل خطوة،
وتذكر دائمًا، كلما طرحت عليك سؤالًا في الآية، كأنني أقول: هل ترى هذا الشيء؟ انظر
إليه، كيف يوجد في بنية النص بشكل متناغم، لدرجة أنك، أحيانًا، لم تكن تشعر به؛ لذلك
حاول أن تغيِّر موقفك!
ولأن عقولنا تتجنب العمل الشاق، وتميل إلى الراحة، فقد نجد، في القصة المشوقة التي ذكرتها حول مسألة "الشكل الرباعي الدائري"، متعة أكبر، وكما أن القصة تعمل على تبديد مثل هذا الخوف، فالأسئلة السهلة، والصغيرة، والمتنوعة قد تعمل هي الأخرى على خلق التحدي اللازم، والاهتمام المطلوب، فهي في حقيقة الأمر ليست "مجرد أسئلة"، وإنما هي كشفٌ لمسارات معرفية، والربط بينها، ومحاولة تفسير للعلاقات بين الأشياء، باستثارة العقل، وتحريضه؛ كي يدرك الدور المنوط به، حتى يسأل أكثر، وحتى يفهم أكثر!
الأسئلة "المتعددة"، و"المتنوعة" في هذا الصدد، نافعة للغاية؛ فهي تمنحك الفرصة، لتغيير وجهة نظرك، وربما تؤدي، بك، إلى تغيير موقفك، في النهاية، ليس بالضرورة أن تجيب عن كل سؤال، وقد يكون، من الجيد لعقلك أن تعجز، عن الإجابة أحيانًا، وقد يكون عجزك، ببساطة، إما لنقص في البيانات، أو لنقص في خبرتك، ومهاراتك، أو معرفتك بقواعد الفن الذي تعمل فيه، لعلي أتذكر معك الآن، عبارة جيدة، جاءت على لسان إحدى شخصيات الكاتب الإنجليزي "أوسكار وايلد" Oscar Wilde، في مسرحية "زوج مثالي": «الأسئلة لن تكون "حمقاء" أبدًا، لكن الإجابات قد تكون أحيانًا»[4]،
ويبقى ابتكار الأسئلة؛ لحل "مشكلة" ما، هو أشبه ما يكون بابتكار "مشكلة" أخرى صغيرة، (وغير محلولة)، لكن قد يساعدك فهمها، وحلها، على فهم المشكلة الأصلية، ومن ثم حلها!
Oscar Wilde, An Ideal Husband (London: Chiswick Press, 1892), p. 14.
قبل نحوٍ عام من الآن، اطلعت، على كتاب لعالم الرياضيات، والأستاذ السابق بجامعة استانفورد، جورجي بوليا، بعنوان (كيف تحلها: How to solve it)، وقد استفدت منه، في صياغتي الجيدة لبعض الأفكار، لا سيما المتعلقة منها، بطرق الاستدلال، (وإن كانت نسخة الكتاب التي حصلت عليها باللغة الإنجليزية؛مع ما فيها من رموز، ومصطلحات رياضية، ما دفعني بطبيعة الحال إلى بذل جهد أكبر، في قراءته)، وأستعير منه هذا "المثال"، عن فائدة "الالتفاف" حول المسألة: «تحاول الحشرة الهروب عبر زجاج النافذة، وتحاول تكرار ذلك، مرة تلو الأخرى، ولا تجرب النافذة التالية المفتوحة، والتي دخلت، من خلالها الغرفة. الإنسان قادر على التصرف بشكل أكثر ذكاء، أو على الأقل يجب أن يكون قادرًا. يتمثل التفوق البشري في "الالتفاف"، حول عقبة، قد لا يمكنه أن يتغلب عليها، بشكل مباشر!»[5].
أضيف إلى ما ذكره أستاذ الرياضيات، في كتابه الرائع، أن "الالتفات" نحو الشيء أمر مطلوب، وضروري تمامًا؛ لأنه إقرار منك بوجوده، وربما كنت لا تعلم بأنه موجود أساسًا، مجرد أن يحدث لك هذا؛ قد يعد اكتشافًا؛ أما "الالتفاف"، حول الشيء، فهو، في حد ذاته أمر ممتع؛ لأنه يمنح العين إحساسًا غنيًّا بالشبع، وإحساسًا غنيًّا بالتنوع، ويجعل التجربة في قراءة النص أكثر إدهاشًا، وتشويقًا؛ كونه يؤدي بنا حتمًا إلى تعدد الزوايا التي ننظر من خلالها إلى الشيء، وفهم ماهيته، كما يؤدي بنا إلى إدراك بعض، من جمال التنوع في الضوء الذي نراه من كل زاوية، مثلما تقلب بيديك "ياقوتة نادرة"، أو "جوهرة نقية"، أو حجرًا كريمًا، يتميز بشدة الجمال والصفاء والنصاعة، وكلما نظرت إليه من زاوية مختلفة؛ كلما بهرتك أضواؤه المنعكسة، وإن كنت لا تستطيع وصف ذلك أحيانًا!
George Pólya, How to solve it: A new aspect of mathematical method. Princeton (Princeton University Press, 2004), p. 51
لأن أرواحنا غالبًا ما تتعلق بأشباهها، وقد يبدو أنَّ عقولنا كذلك، ولهذا فإن للأستاذ جمال البدراوي، فضله الكبير عليَّ، وعلى كثيرين غيري، بما كان وما زال يتمتع به من جمال الروح، وسرعة البديهة، وذكاء الخاطر، وبما يعرف عنه من محبة حقيقية للعلم، ولاكتسابه، ومن قدرة دائمة على تحفيز طلابه، وتوثيق علاقته بهم، ومنحهم التحدي اللازم والاهتمام المطلوب؛ لذلك كانت هذه الصفحة، بمثابة نوع من الامتنان المستحق لشخصه الكريم، ولأشخاص ملهمين آخرين ، سأذكرهم تباعًا، (وهي مأخوذة بالمناسبة بتصرف يسير من أحد فصول الكتاب، والذي جعلته بعنوان: "متعة الفهم، والكشف، ودهشة التأويل"، كون هؤلاء، هم بعض أولئك الذين أدين لهم بالفضل، ومن أكثر الأشخاص الذي التقيت بهم، ذكاءً، وتفهمًا، وإدراكًا!